机器学习要素#

机器学习定义#

机器学习的目标是：通过观测数据$(x, y)$, 让算法从假设集$H$中自动寻找一个假设函数$g(x)$, 使其尽可能接近真实目标函数$f(x)$.

• 关键对比：传统编程是“人为定义规则”（如手动设计电影评分公式）, 而机器学习是“逆向工程”——从数据（观众评分）反推规则（哪些因素影响评分）.

• 示例：预测电影评分时, 机器学习不依赖“导演名气+演员阵容”等人为设定, 而是通过历史评分数据, 让算法自动发现观众的潜在偏好（如偏爱科幻片或剧情片）.

机器学习组成要素#

$(\mathscr{X},\mathscr{Y},f,H,A)$

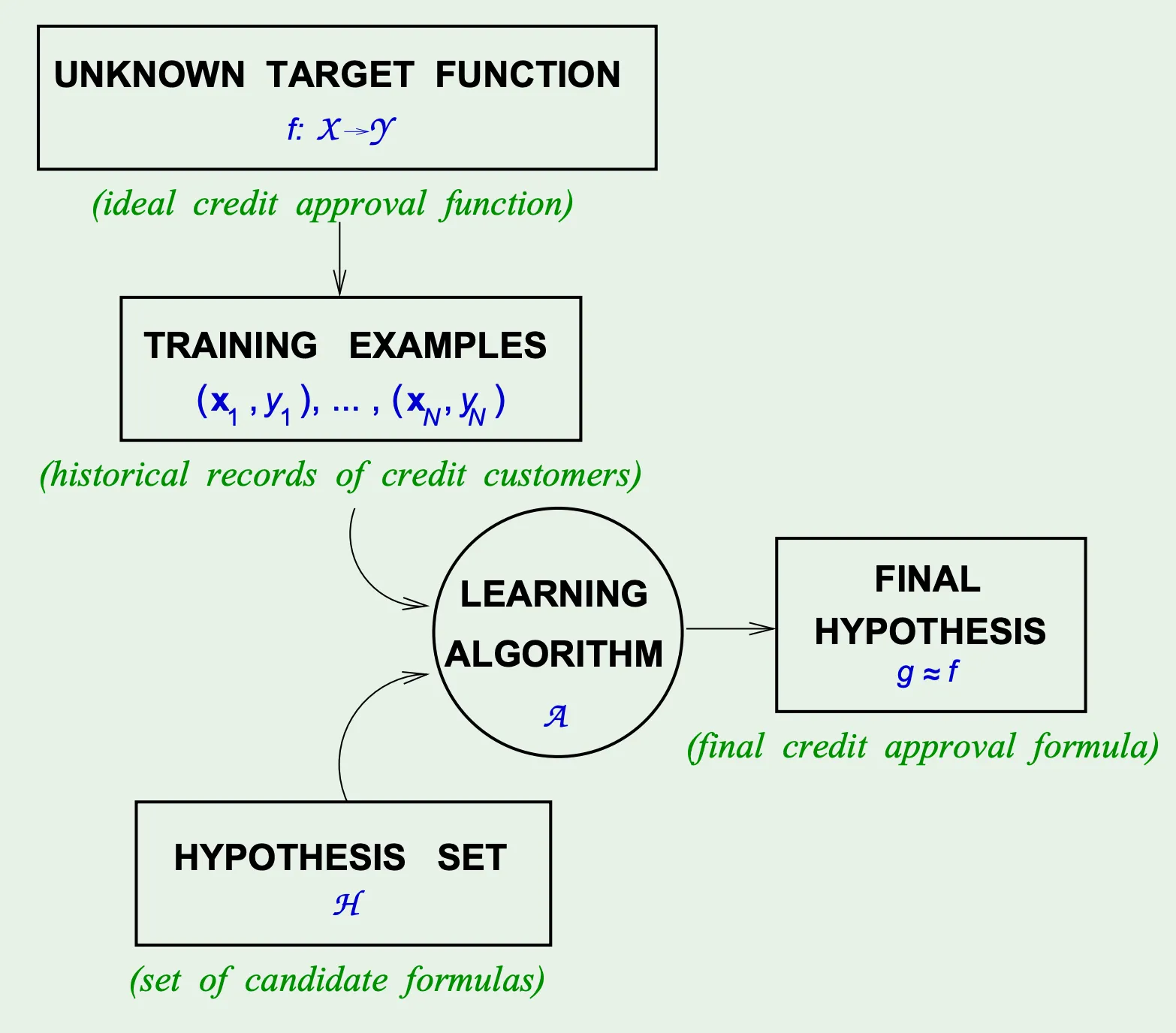
输入空间与输入特征#

输入空间$\mathscr{X}$与输入特征$x$

• 定义：$x \in \mathscr{X}$, $\mathscr{X}$ 是所有可能输入的特征空间

• 描述：输入特征向量由算法处理的原始属性构成, 决定模型的感知范围

• 例子:

  • 电影推荐：$\mathscr{X} = \mathbb{R}^2$（二维空间）, $x = [\text{类型编码}, \text{时长（分钟）}]$

  • 具体输入：$x = [1, 120]$（1表示科幻片, 120分钟）

输出空间与标签#

输出空间$\mathscr{Y}$与标签$y$

• 定义：$y \in \mathscr{Y}$, $\mathscr{Y}$ 是目标变量的取值范围

• 描述：监督学习的目标值, 分为分类（离散）或回归（连续）

• 例子:

  • 回归任务：$\mathscr{Y} = [1, 5]$, $y = 4.5$（对应$x=[1, 120]$的电影评分）

  • 分类任务：$\mathscr{Y} = \{-1, +1\}$, $y = +1$（PLA算法:“推荐/不推荐”的二分类）

数据集#

数据集 $D = \{(x_i, y_i)\}_{i=1}^n$

• 定义：从真实分布 $P(x, y)$ 独立同分布采样的训练集

• 例子：

  • 生成方式：$D$ 由$f$ 生成并添加噪声（如电影评分受“观众情绪”噪声影响）

  • 规模影响：$n=10$ 时PLA可能过拟合, $n=1000$ 时更接近$f$

目标函数#

目标函数$f: \mathscr{X} \to \mathscr{Y}$（未知）

• 定义：数据生成的真实映射关系, 无法显式获取

• 例子：

  人工生成数据$f(x) = \text{sin}(2\pi x) + \text{噪声}$, 算法通过多项式拟合尝试逼近

假设集和假设函数#

假设集$\mathscr{H}$和假设函数$g: \mathscr{X} \to \mathscr{Y}$（已知）

用于近似$f$

• 数学形式：

  • 线性分类：$g(x) = \text{sign}(w \cdot x + b)$（PLA算法）

  • 线性回归：$g(x) = w \cdot x + b$（$w = (X^TX)^{-1}X^Ty$）

• 例子：

  用$g(x) = 0.8x_1 - 0.01x_2 + 2$ 预测电影评分, $x_1$（类型）权重为正, $x_2$（时长）权重为负, 对应“科幻片加分、长电影减分”的归纳

• 感知机

For input $x = (x_1, \cdots, x_d)$ ‘attributes of a customer’

这个集合可以包括：收入, 居住年限等等

This linear formula $h \in \mathcal{H}$ can be written as

Introduce an artificial coordinate $x_0 = 1$:

In vector form, the perceptron implements

学习算法#

$\mathscr{A}$：从$D$到$g$的优化过程

• PLA算法：

  • 步骤：初始化$w$, 遍历$D$, 误分类时更新$w \leftarrow w + y_i x_i$

  • 终止条件：$E_{\text{in}}(g) = 0$

• 最小二乘法：

  • 目标：$\min_w \sum_{i=1}^n (y_i - w \cdot x_i)^2$

  • 解：$w = (X^TX)^{-1}X^Ty$

$\mathscr{A}$和$\mathscr{H}$放在一起叫做学习模型.

三大学习#

监督学习：有人教“这是对的”（如父母教孩子“红灯停”）.

无监督学习：自己发现“哪些相似”（如孩子把玩具按颜色分类）.

强化学习：试错后知道“这样做更好”（如孩子学骑车, 摔了知道要平衡）.

监督学习#

定义：用带标签的数据（如“垃圾邮件/正常”“房价100万”）, 学输入到输出的映射.

核心：从“已知答案”中模仿规律, 目标是预测新数据的标签.

例子：

• 分类：售货机识别硬币——提前输入“1元硬币=可乐”“5角硬币=退币”, 学会后根据投币面值吐对应商品.

• 回归：预测奶茶销量——输入天气温度（28℃/32℃）和历史销量（300杯/500杯）, 学温度与销量的关系.

无监督学习#

定义：用无标签数据（如用户消费记录、像素点）, 自己找内在结构（分组/模式）.

核心：在“没有答案”的情况下, 发现数据的隐藏规律（如相似性、特征压缩）.

例子：

• 聚类：售货机分析投币习惯——收集1000次投币数据（时间、金额）, 自动分成“早高峰1元组”和“下午茶5元组”.

• 降维：压缩商品图片——将1000维像素数据降到50维, 保留“饮料瓶形状”“零食包装颜色”等关键特征.

强化学习#

定义：通过试错互动（行动→环境反馈奖惩）, 学最大化长期奖励的策略.

核心：在动态环境中“边做边学”, 奖惩是唯一指导（无直接标签）.
例子：

• 机器人补货：售货机缺货时, 机器人尝试不同路径（左/右/中间）, 快到货架+5分, 撞人-3分, 最终学会“绕开人流高峰的最短路径”.

• 游戏AI：自动玩推箱子, 推到目标+10分, 超时-5分, 通过上万次尝试, 找到“先卡位再推”的最优策略.

参数估计#

矩估计#

设总体 $X$ 的 $k$ 阶原点矩为 $\mu_k = E(X^k)$, 样本 $X_1, X_2, \cdots, X_n$ 的 $k$ 阶原点矩为 $A_k=\frac{1}{n}\sum_{i = 1}^{n}X_i^k$.

• 用样本矩估计总体矩：令总体的 $k$ 阶原点矩等于样本的 $k$ 阶原点矩, 即 $\mu_k = A_k$ .

• 求解参数估计值：假设总体分布中有 $m$ 个未知参数 $\theta_1, \theta_2, \cdots, \theta_m$, 可以列出 $m$ 个方程 $\mu_{k_j}=A_{k_j}$（$j = 1, 2, \cdots, m$）, 然后联立求解这 $m$ 个方程, 得到的 $\theta_1, \theta_2, \cdots, \theta_m$ 的值就是矩估计值 $\hat{\theta}_{1\_ME}, \hat{\theta}_{2\_ME}, \cdots, \hat{\theta}_{m\_ME}$ .

• 如总体均值 $\mu = E(X)$, 用样本均值 $\bar{X}=\frac{1}{n}\sum_{i = 1}^{n}X_i$ 来估计；总体方差 $\sigma^2 = E((X - E(X))^2)=E(X^2)-[E(X)]^2$, 用 $S^2=\frac{1}{n}\sum_{i = 1}^{n}(X_i - \bar{X})^2$ （或 $S_n^2=\frac{1}{n - 1}\sum_{i = 1}^{n}(X_i - \bar{X})^2$ , 无偏估计）来估计.

最大似然估计#

假设样本 $X_1, X_2, \cdots, X_n$ 是独立同分布的, 其概率密度函数（或概率质量函数）为 $f(x;\theta)$, 其中 $\theta$ 是待估计的参数向量.

• 似然函数： $L(\theta)=\prod_{i = 1}^{n}f(X_i;\theta)$

• 对数似然函数：为了计算方便, 通常对似然函数取对数得到对数似然函数 $\ln L(\theta)=\sum_{i = 1}^{n}\ln f(X_i;\theta)$

• 求解最大似然估计值：通过对对数似然函数求关于 $\theta$ 的导数（若 $\theta$ 是多维向量, 则求偏导数）, 并令导数为 0, 即 $\frac{\partial \ln L(\theta)}{\partial \theta}=0$ 求解上述方程, 得到的 $\theta$ 值就是最大似然估计值 $\hat{\theta}_{MLE}$ .

贝叶斯估计#

设 $\theta$ 是待估计的参数, $X$ 是观测数据.

• 贝叶斯定理： $P(\theta|X)=\frac{P(X|\theta)P(\theta)}{P(X)}$

• $P(\theta|X)$ 是后验概率, 表示在观测到数据 $X$ 的条件下, 参数 $\theta$ 的概率；

• $P(X|\theta)$ 是似然函数, 表示在参数为 $\theta$ 的条件下, 观测到数据 $X$ 的概率；

• $P(\theta)$ 是先验概率, 表示在没有观测到数据 $X$ 之前, 对参数 $\theta$ 的概率分布的认识；

• $P(X)$ 是证据因子, 是一个与 $\theta$ 无关的归一化常数, $P(X)=\int P(X|\theta)P(\theta)d\theta$ （对于连续型参数）或 $P(X)=\sum_{\theta} P(X|\theta)P(\theta)$ （对于离散型参数）.

• 贝叶斯估计值：常见的贝叶斯估计值可以通过后验概率的期望来计算, 即

对于离散型参数, 则为 $\hat{\theta}_{BE}=\sum_{\theta} \theta P(\theta|X)$ . 此外, 也可以取后验概率的最大值点（即最大后验估计, MAP）作为估计值 .

决策理论#

掌握数据的潜在概率分布

损失(预测差异标准)#

01损失#

• 定义：$\ell(y, z) = 1_{y\neq z}$ , 即当预测值 $z$ 与真实值 $y$ 相等时（无错误）, 损失为 $0$ ；当预测值 $z$ 与真实值 $y$ 不相等时（有错误）, 损失为 $1$ .
• 适用场景：主要用于分类问题.

平方损失#

• 定义：$MSE = \frac{1}{n}\sum_{i = 1}^{n}(y_i - \hat{y}_i)^2$, 其中$y_i$是真实值, $\hat{y}_i$是预测值, $n$是样本数量.
• 适用场景：常用于回归问题, 能直观反映预测值与真实值的平均偏离程度, 对较大误差惩罚较重.

绝对损失#

• 定义：$MAE = \frac{1}{n}\sum_{i = 1}^{n}|y_i - \hat{y}_i|$.
• 适用场景：也用于回归问题, 对异常值相对不敏感, 能更稳健地反映预测值与真实值的平均误差

交叉熵损失#

• 定义：对于二分类问题, $L = -[y\log\hat{y}+(1 - y)\log(1 - \hat{y})]$；对于多分类问题, $L = -\sum_{i = 1}^{n}y_i\log\hat{y}_i$, 其中$y$是真实标签, $\hat{y}$是预测的概率分布.
• 适用场景：主要用于分类问题, 尤其是在处理概率输出的模型如逻辑回归、神经网络等中广泛应用, 能很好地衡量两个概率分布之间的差异.

Hinge损失#

• 定义：$L = \max(0, 1 - y\hat{y})$, 常用于支持向量机（SVM）中.
• 适用场景：适用于二分类问题, 它鼓励分类器找到一个能将不同类别数据很好分隔开的决策边界, 使得正确分类的样本距离边界有一定的 margin.

风险(性能评判标准)#

期望风险#

给定一个预测函数$f:\mathcal{X} \to \mathcal{Y}$、一个损失函数$\ell:\mathcal{Y} \times \mathcal{Y} \to \mathbb{R}$以及一个联合分布$p(x, y)$, 预测函数$f$的期望风险定义为：

作用：期望风险反映了模型在整个数据分布上的平均损失情况, 期望风险越低, 通常意味着模型的泛化能力越强, 更有可能在实际应用中取得较好的预测结果.

经验风险(训练误差)#

给定一个预测函数$f:\mathcal{X} \to \mathcal{Y}$、一个损失函数$\ell:\mathcal{Y} \times \mathcal{Y} \to \mathbb{R}$以及一组训练数据$(x_i, y_i) \in \mathcal{X} \times \mathcal{Y}$, 其中$i = 1,\ldots,n$, 预测函数$f$的经验风险定义为：

作用：经验风险衡量模型在训练数据上的拟合程度. 训练时, 常通过最小化经验风险调整参数, 让模型适配训练数据. 但单纯追求最小化易引发过拟合, 模型会过度学习噪声与特殊情况, 忽视数据整体分布, 所以无法完全体现模型的泛化能力 .

超额风险#

设模型$f$的期望风险为$R(f)$, 最优风险（即所有可能模型中最小的期望风险）为$R^*$, 那么超额风险$\Delta R$定义为：

作用：超额风险用于评估学习算法所得模型与理论最优模型的差距, 能直观反映模型在泛化能力上的提升空间. 它帮助研究者与工程师判断模型性能, 若超额风险大, 意味着当前模型距最优有较大改进空间, 此时可通过调整模型结构、增加训练数据量或选用更优学习算法等方式优化模型 .

固定设计风险#

输入变量$x$是固定的, 不随样本变化而随机变动. 假设我们有固定的输入点$x_1, x_2, \ldots, x_n$, 以及对应的输出$y_i$. 对于预测函数$f:\mathcal{X} \to \mathcal{Y}$和损失函数$\ell:\mathcal{Y} \times \mathcal{Y} \to \mathbb{R}$, 固定设计风险定义为：

这里的期望是针对输出$y_i$的分布（在给定固定输入$x_i$的条件下）.

作用：固定设计风险可评估模型在此特定条件下对输出的预测准确性. 能展现模型在固定输入环境中的性能, 助力在该场景下筛选合适模型、判断模型对特定输入的适应性. 并且, 分析固定设计风险随模型参数等因素的变化, 可优化模型在此场景下的性能 .

随机设计风险#

输入变量$x$是随机的, 服从某个分布$p(x)$. 对于预测函数$f:\mathcal{X} \to \mathcal{Y}$、损失函数$\ell:\mathcal{Y} \times \mathcal{Y} \to \mathbb{R}$以及联合分布$p(x, y)$, 随机设计风险定义为：

其中$\mathbb{E}_{y|x}$表示在给定$x$条件下对$y$的期望, $\mathbb{E}_{x}$表示对$x$的期望.

作用：随机设计风险可评估模型对随机输入的泛化能力, 判断其能否适应不同输入并维持良好预测性能. 鉴于真实环境数据多具随机性, 这对模型实际应用意义重大. 它有助于筛选在随机输入下表现最佳的模型, 还能评估模型在复杂多变现实环境中的可靠性与稳定性.

贝叶斯风险#

将未知参数视为随机变量, 强调基于已有信息（先验知识）和观测数据进行推断. 在贝叶斯体系里, 先验知识通过先验分布 $P(\theta)$ 体现, 它代表在未接触观测数据之前, 我们对参数 $\theta$ 的不确定性认知. 当获取到观测数据 $X$ 后, 运用贝叶斯定理

$P(\theta|X)=\frac{P(X|\theta)P(\theta)}{P(X)}$

更新先验分布, 从而得到后验分布 $P(\theta|X)$. 其中, $P(X|\theta)$ 为似然函数, 描述在参数为 $\theta$ 时观测到数据 $X$ 的概率；$P(X)$ 作为证据因子, 用于对后验分布进行归一化处理. 通过这种方式, 我们能依据不断积累的信息, 持续更新对参数的认知.

先验估计#

先验估计即确定先验分布 $P(\theta)$ 的过程. 先验分布的设定可基于过往经验、领域专业知识或合理假设.

例如, 在估计一枚硬币正面朝上的概率 $\theta$ 时, 若毫无额外信息, 我们可能采用均匀分布作为先验分布, 意味着在观测数据前, 认为 $\theta$ 取任何值的可能性均等.

若已知该硬币是正常硬币, 大概率会将先验分布设定为以 0.5 为中心的较为集中的分布, 反映对硬币正面朝上概率接近 0.5 的先验认知.

后验估计#

后验估计是在依据观测数据 $X$ 得到后验分布 $P(\theta|X)$ 后, 对参数 $\theta$ 进行估计的过程. 常见方法主要有两种：

最大后验估计（MAP）：选取后验分布中概率最大的参数值作为估计值.

基于后验期望的估计：计算参数 $\theta$ 在给定后验分布下的期望值作为估计值. 后验估计融合了先验信息与观测数据, 相较于单纯的先验估计, 能更精准反映参数的真实状况.

在贝叶斯框架下, 结合数据的联合分布 $p(x, y)$, 以及预测函数 $f:\mathcal{X} \to \mathcal{Y}$ 和损失函数 $\ell:\mathcal{Y} \times \mathcal{Y} \to \mathbb{R}$, 贝叶斯风险的定义为：

作用

评估性能：作为评估模型性能的基准, 对比实际模型风险与贝叶斯风险, 基于贝叶斯框架对不确定性的处理, 判断模型性能提升空间.

指导选型：模型选择时, 优先考虑风险接近贝叶斯风险的模型, 因其更趋近理论最优, 泛化能力和预测准确性更佳, 能更好利用先验与数据信息.

助力改进：模型改进时, 若模型风险远高于贝叶斯风险, 可重新审视先验分布设定或调整模型结构, 以优化数据拟合效果, 因为先验分布影响后验推断和预测风险

贝叶斯预测器(最佳预测函数)#

推导#

利用条件期望及全期望公式：

给定对于任意$x' \in \mathcal{X}$ 的条件分布, 即$y|x = x'$, 为任意$z \in \mathcal{Y}$ 定义条件风险：

由此可得

期望风险在贝叶斯预测器$f^*:\mathcal{X} \to \mathcal{Y}$ 处达到最小, 对于所有$x' \in \mathcal{X}$,

贝叶斯风险$\mathcal{R}^*$ 是所有贝叶斯预测器的风险, 且等于：

常用的贝叶斯预测器#

0 - 1损失：

• 对于$\mathcal{Y} = \{0, 1\}$ 和$\ell(y,z) = 1_{y\neq z}$, 贝叶斯预测器满足：

• 记$\eta(x') = \mathbb{P}(y = 1|x = x')$, 如果$\eta(x') > 1/2$, $f^*(x') = 1$；而如果$\eta(x') < 1/2$, $f^*(x') = 0$. 当$\eta(x') = 1/2$ 时, 结果无关紧要.
• $\mathcal{R}^*=\mathbb{E}[\min\{\eta(x),1 - \eta(x)\}]$, 一般来说它严格为正（除非$\eta(x) \in \{0, 1\}$ 几乎必然成立, 即$y$ 是$x$ 的确定性函数）.
• 当$k \geq 2$ 时$\mathcal{Y} = \{1,\ldots,k\}$, 此时$f^*(x') \in \arg\max_{i \in \{1,\ldots,k\}}\mathbb{P}(y = i|x = x')$ .

平方损失：

• 对于$\mathcal{Y} = \mathbb{R}$ 和$\ell(y,z) = (y - z)^2$, 贝叶斯预测器满足：

• 得到条件期望$f^*(x') = \mathbb{E}(y|x = x')$ .

绝对损失：

• 对于$\mathcal{Y} = \mathbb{R}$ 和$\ell(y,z)=|y - z|$, 贝叶斯预测器满足： $f^*(x') \in \arg\min_{z \in \mathbb{R}}\mathbb{E}[|y - z||x = x']$
  • 可以证明此时$f^*(x')$ 是条件中位数, 即$f^*(x')$ 满足$\mathbb{P}(y \leq f^*(x')|x = x') \geq \frac{1}{2}$ 且$\mathbb{P}(y \geq f^*(x')|x = x') \geq \frac{1}{2}$ .

Hinge损失：

• 对于二分类问题$\mathcal{Y}=\{-1,1\}$, Hinge损失函数定义为$\ell(y,z)=\max(0,1 - yz)$ .
• 贝叶斯预测器$f^*(x') \in \arg\min_{z \in \{-1,1\}}\mathbb{E}[\max(0,1 - yz)|x = x']$ .
• 记$p=\mathbb{P}(y = 1|x = x')$, $1 - p=\mathbb{P}(y=-1|x = x')$, 则$\mathbb{E}[\max(0,1 - yz)|x = x']=p\max(0,1 - z)+(1 - p)\max(0,1 + z)$ .
• 当$p>\frac{1}{2}$ 时, $f^*(x') = 1$；当$p<\frac{1}{2}$ 时, $f^*(x')=-1$；当$p = \frac{1}{2}$ 时, 选择$z = 1$ 或$z=-1$ 对风险没有影响 .

通过对不同损失函数下贝叶斯预测器的分析, 我们可以根据具体问题选择合适的损失函数和预测器, 以最小化期望风险.

统计学习理论#

学习理论的目标是为模型在未见数据上的性能提供一定的保障. 假设数据$\mathcal{D}_{n}(dp)=\{(x_1, y_1),\ldots,(x_n, y_n)\}$ 是从分布族$\mathcal{P}$ 中某个未知分布$dp$ 进行独立同分布（i.i.d.）采样得到的观测值.

目标是找到这样的算法$\mathcal{A}$ ：$\mathcal{A}$ 是一个从$\mathcal{D}_{n}(dp)$（对于任意$n$）到一个从$\mathcal{X}$ 到$\mathcal{Y}$ 的函数的映射, 风险取决于概率分布$dp \in \mathcal{P}$, 表示为$\mathcal{R}_{dp}(f)$ .

性能度量#

期望误差#

• 定义：$\mathbb{E}\left[\mathcal{R}_{dp}(\mathcal{A}(\mathcal{D}_{n}(dp)))\right]$, 其中期望是关于训练数据的.

• 一致性判断：对于分布$dp$, 如果当$n$趋于无穷时, $\mathbb{E}\left[\mathcal{R}_{dp}(\mathcal{A}(\mathcal{D}_{n}(dp)))\right] - \mathcal{R}_{dp}^*$趋于$0$, 则称算法$\mathcal{A}$在期望上是一致的.

• “可能近似正确”（PAC）学习：对于给定的$\delta \in (0, 1)$和$\varepsilon > 0$：

关键在于找到尽可能小的$\varepsilon$（通常是$\delta$的函数）. PAC一致性的概念是指, 对于任意$\varepsilon > 0$, 对于每个$n$ 都有这样一个不等式成立, 并且存在一个趋于$0$的序列$\delta_{n}$ .

没有免费的午餐定理#

定理（固定$n$）： 考虑带有0 - 1损失的二分类问题, 其中$\mathcal{X}$ 是无限集. 设$\mathcal{P}$ 表示$\mathcal{X} \times \{0, 1\}$ 上所有概率分布的集合. 对于任意$n > 0$ 和学习算法$\mathcal{A}$,

该定理指出, 不存在一个能在所有分布上都最优运行的学习算法. 也就是说, 在机器学习中, 没有假设的情况下学习是不可能的. 这打破了我们对于找到一个通用的完美算法的幻想.

证明的主要思路:

(a) 构造一个支撑在$\mathbb{N}$ 中$k$ 个元素上的概率分布, 其中$k$ 相较于固定的$n$ 很大, 并证明$n$ 个标签的信息并不能保证在所有$k$ 个元素上都表现良好；

(b) 通过与由随机参数得到的性能进行比较来选择该分布的参数（下面的向量$r$）.

定理 (误差序列): 考虑带有0 - 1损失的二分类问题, 其中$\mathcal{X}$ 是无限集. 设$\mathcal{P}$ 表示$\mathcal{X} \times \{0, 1\}$ 上所有概率分布的集合. 对于任意趋于$0$ 的递减序列$a_n$ , 且满足$a_1 \leq 1/16$, 对于任意学习算法$\mathcal{A}$ , 存在$dp \in \mathcal{P}$ , 使得对于所有$n \geq 1$：

证明: 设$k$ 为正整数. 不失一般性, 我们可以假设$\mathbb{N} \subset \mathcal{X}$.

给定$r \in \{0, 1\}^k$, 我们在$(x, y)$ 上定义联合分布$dp$, 使得对于

也就是说, 对于$x$, 我们从$k$ 个元素中均匀随机地选择一个, 然后$y$ 被选定为$y = r_x$. 因此贝叶斯风险为$0$（因为存在确定性关系）：$\mathcal{R}_{dp}^* = 0$.

记$\widehat{f}_{\mathcal{D}_{n}} = \mathcal{A}(\mathcal{D}_{n}(dp))$ 为分类器, $S(r) = \mathbb{E}[\mathcal{R}_{dp}(\widehat{f}_{\mathcal{D}_{n}})]$ 为期望风险, 我们想要关于$r \in \{0, 1\}^k$ 最大化$S(r)$；这个最大值大于$r$ 上任意分布$dq$ 下$S(r)$ 的期望, 特别是均匀分布（每个$r_j$ 是独立无偏的伯努利变量）. 那么

因为$x$ 几乎必然在$\{1,\ldots,k\}$ 中, 且$y = r_x$ 几乎必然成立. 注意我们是关于$x_1,\ldots,x_n,x$ 和$r$ 取期望（它们相互独立）.

因为$\mathbb{P}(\widehat{f}_{\mathcal{D}_{n}}(x) \neq r_x|x \notin \{x_1,\ldots,x_n\},x_1,\ldots,x_n,r_{x_1},\ldots,r_{x_n}) = 1/2$（在$x$ 未被观测到的情况下, 标签$x = r_x$ 为$0$ 或$1$ 的概率相同）. 因此,

给定$n$, 我们可以让$k$ 趋于无穷来得出结论.

评估方法#

交叉验证#

• K折交叉验证：将数据集分为K个互不重叠子集, 轮流以一个子集为测试集, 其余为训练集, 重复K次, 取平均评估模型.

• 留一交叉验证（LOOCV）：K等于样本总数, 每次用一个样本做验证, 其余做训练, 遍历所有样本

• 分层交叉验证：适用于分类任务, 保证每个折内类别分布与整体一致, 避免类别失衡影响评估.

• 时间序列交叉验证：用于时间序列数据, 按时间顺序划分, 防止数据泄漏, 保证评估真实性.

• 嵌套交叉验证：包含内外层, 外层评估模型泛化性, 内层用于超参数优化.

取出测试集, 剩下的(A,B,C,D,E)当训练集和验证集, 第一次A当验证, BCDE训练. 第二次B当验证, ACDE训练…