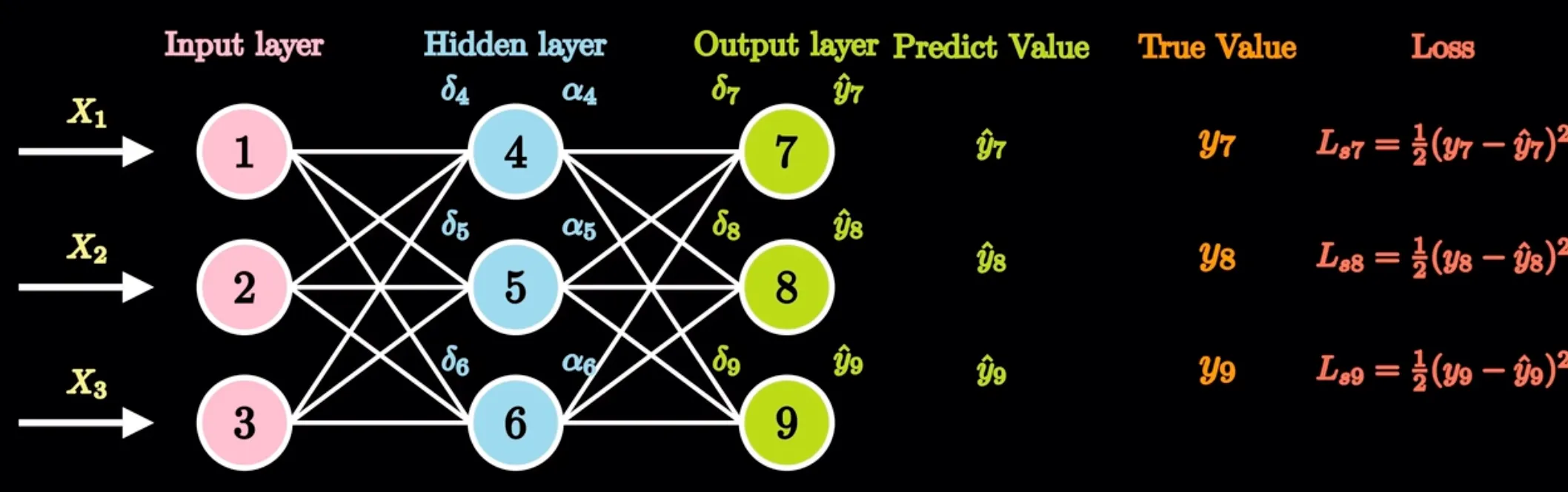
符号含义#

输入层#

• 输入: $x_1,x_2,x_3$

隐藏层#

• 输入：$\delta_4, \delta_5, \delta_6$
• 激活值：$\alpha_4, \alpha_5, \alpha_6$

输出层#

• 输入：$\delta_7, \delta_8, \delta_9$
• 预测值：$\hat{y}_7, \hat{y}_8, \hat{y}_9$

其他#

• 真实值：$y_7, y_8, y_9$
• 学习率: $\eta$
• 激活函数: $\sigma(x)$, $\sigma(x)=\frac{1}{1+e^{-x}}$
• 损失函数：$L_{s7}, L_{s8}, L_{s9}$, $L_{s}=\frac{1}{2}(y - \hat{y})^2$
• 权重: $\omega_{ij}$ (如神经元1, 4, 权重$\omega_{14}$)

正向传播#

已知内容

• 输入数据：输入层的 $x_1$、$x_2$、$x_3$, 它们是网络接收的初始信息.

• 权重: $\omega_{ij}$ (如神经元1, 4, 权重$\omega_{14}$), 决定了信号传递的强度.

• 激活函数: $\sigma(x)$, $\sigma(x)=\frac{1}{1+e^{-x}}$

• 损失函数：$L_{s}=\frac{1}{2}(y - \hat{y})^2$

• 真实值：即 $y_7$、$y_8$、$y_9$ , 可用于后续评估预测结果, 但不参与正向传播计算本身.

需求内容

• 隐藏层激活值： $\alpha_4$、$\alpha_5$、$\alpha_6$ 这类隐藏层神经元经过加权求和并通过激活函数后的输出值.

• 输出层预测值： $\hat{y}_7$、$\hat{y}_8$、$\hat{y}_9$ , 这是网络针对输入数据给出的最终预测结果, 是正向传播的主要计算目标.

• 损失值（间接需求）：虽然不是正向传播直接计算得出, 但正向传播得到预测值后, 结合真实值（如 $y_7$、$y_8$、$y_9$ ）, 利用损失函数（如 $L_{s_7}$、$L_{s_8}$、$L_{s_9}$ 对应的均方误差公式 ）计算出损失值, 用于评估模型性能和后续反向传播优化

反向传播#

在这张图所示的神经网络反向传播过程中：

已知内容#

• 正向传播结果：包括隐藏层激活值（如$\alpha_4$、$\alpha_5$、$\alpha_6$）和输出层预测值（如$\hat{y}_7$、$\hat{y}_8$、$\hat{y}_9$）

• 真实值：$y_7$、$y_8$、$y_9$

• 学习率: $\eta$

• 损失函数：$L_{s}=\frac{1}{2}(y - \hat{y})^2$

• 权重: $\omega_{ij}$ (如神经元1, 4, 权重$\omega_{14}$), 决定了信号传递的强度.

• 激活函数: $\sigma(x)$, $\sigma(x)=\frac{1}{1+e^{-x}}$

要求内容#

• 更新权重：$\hat{\omega_{ij}}$ 根据计算得到的权重梯度和学习率, 对权重进行更新

更新隐藏层和输出层的权重 (举例神经元4)

更新输入层和隐藏层的权重 (举例神经元1)